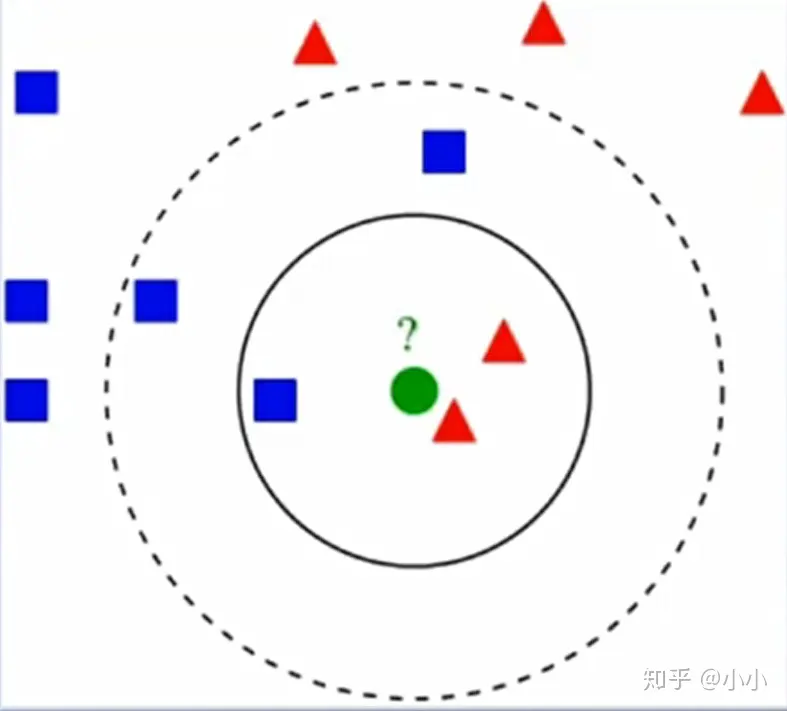
算法
- 输入:训练数据集$T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$,其中$x_i\in \chi \subseteq \pmb{R}^n$为实例的特征向量,$y_i\in Y=\{c_1,c_2,...,c_N\}$为实例的类别
- 输出:实例x所属的类别y。
- 根据给定的距离度量,在训练集T中找出与x最邻近的k个点,涵盖这k个点的x的邻域记作$N_k(x)$;
在$N_k(x)$中根据分类决策规则(如多数表决)决定x的类别y:
$$ y=arg\underset{c_j}max\displaystyle \sum_{x_i\in N_k(x)}I(y_i==c_j),\quad i=1,2,3,..,N;j=1,\\2,3,...,N. $$
其中I为指示函数,当$y_i=c_j$时,I为1,否则为0
距离度量
- $L_p(x_i,x_j)=(\displaystyle \sum_{l=1}^n|x_i^{(l)}-x_j^{(l)}|)^{\frac{1}{p}}$
- 当p=2时,称为欧氏距离
- 当p=1时,称为曼哈顿距离
- 当p=$\infty$时,它是各个坐标距离的最大值,即$$L_\infty(x_i,x_j)=\underset {l}{max}|x_i^{(l)}-x_j^{(l)}|$$
- sklearn API
class sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, *, weights='uniform', algorithm='auto', leaf_size=30, p=2, metric='minkowski', metric_params=None, n_jobs=None, **kwargs)- 参数具体使用方法,看这里
